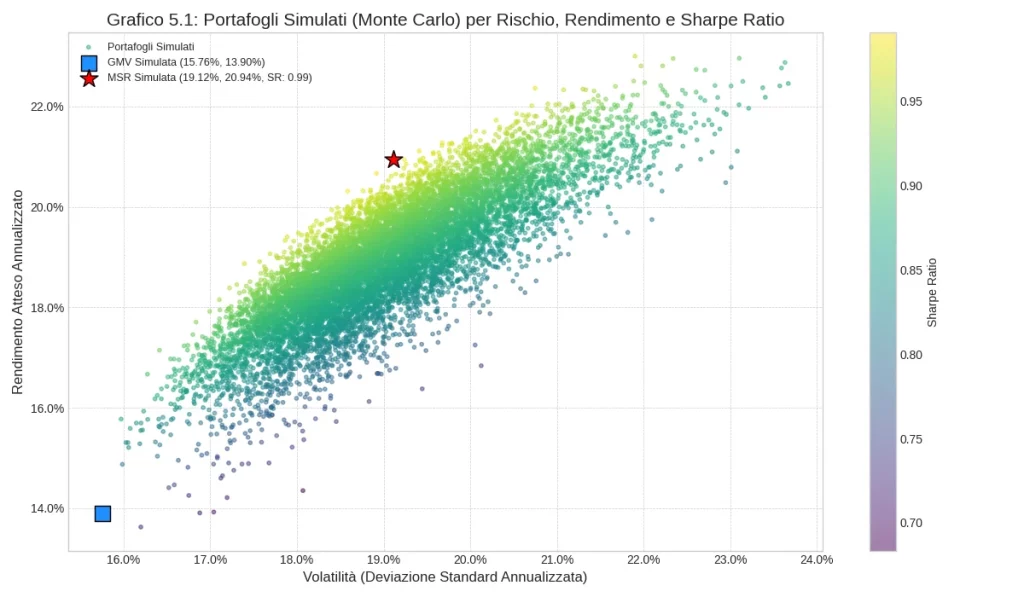
“Grafico 5.1: Portafogli Simulati con il metodo Monte Carlo, visualizzati per Rischio (Volatilità), Rendimento Atteso Annualizzato e Sharpe Ratio. Sono indicati il Portafoglio a Varianza Minima Globale (GMV) e il Portafoglio con Massimo Sharpe Ratio (MSR).”

🟦 1. Introduzione generale

Benvenuti a questa analisi approfondita dedicata a uno dei pilastri della finanza quantitativa moderna: la Frontiera Efficiente di Markowitz. In un mondo finanziario sempre più complesso e interconnesso, la capacità di costruire portafogli di investimento che bilancino in modo ottimale rischio e rendimento non è solo auspicabile, ma fondamentale. Questo studio si propone di demistificare e rendere applicabile la Teoria Moderna di Portafoglio (MPT) formulata dal premio Nobel Harry Markowitz, un corpus teorico che ha rivoluzionato l’approccio alla gestione degli investimenti introducendo il concetto scientifico di diversificazione. Non si tratta semplicemente di “non mettere tutte le uova nello stesso paniere”, ma di comprendere come le interazioni tra diversi asset possano essere sfruttate per massimizzare i rendimenti attesi per un dato livello di rischio, o, viceversa, minimizzare il rischio per un dato livello di rendimento. L’importanza strategica di questo studio risiede nella sua capacità di fornire un framework razionale e quantitativo per le decisioni di asset allocation, allontanandosi da approcci puramente intuitivi o basati su singole scommesse.

Lo studio che presenteremo non è un mero esercizio accademico; è una disamina pratica e operativa, pensata per fornire strumenti concreti e una comprensione profonda. Analizzeremo come, partendo da dati storici di prezzo di un insieme selezionato di asset, sia possibile calcolare rendimenti attesi, volatilità, covarianze e, infine, costruire la frontiera efficiente. Questa frontiera non è un concetto astratto, ma una curva tangibile che rappresenta l’insieme di tutti i portafogli ottimali. Identificheremo inoltre due portafogli particolarmente significativi: il Portafoglio a Varianza Minima (MVP), che, come suggerisce il nome, minimizza il rischio complessivo, e il Portafoglio Tangente, cruciale quando si introduce un asset privo di rischio e fondamentale per la costruzione della Capital Market Line (CML). L’obiettivo è quello di passare da dati grezzi a una comprensione visiva e quantitativa delle opportunità di investimento, un percorso essenziale per chiunque operi sui mercati con un approccio sistematico.

La scelta degli asset per questo studio – specificamente un portafoglio di 10 ticker azionari statunitensi di grande capitalizzazione (MSFT, AAPL, GOOGL, AMZN, JNJ, V, JPM, PG, NVDA, HD) – non è casuale. Questi titoli rappresentano una porzione significativa del mercato globale, appartengono a settori diversi (tecnologia, beni di consumo, finanza, sanità) e sono caratterizzati da liquidità elevata e ampia disponibilità di dati storici. Analizzare un tale insieme di asset permette di illustrare efficacemente i benefici della diversificazione tra società con fondamentali e dinamiche di mercato differenti. Inoltre, la familiarità di molti investitori con questi nomi rende l’analisi più relatable e le conclusioni più facilmente contestualizzabili. L’utilizzo di dati storici per il periodo compreso tra il 1 Gennaio 2015 e il 31 Dicembre 2024 garantisce un orizzonte temporale sufficientemente lungo da includere diverse fasi di mercato, comprese quelle di alta volatilità e di crescita sostenuta, rendendo l’analisi più robusta. A questi si aggiunge un tasso risk-free del 2.09% annuo, derivato dall’indice ^IRX, per completare il quadro necessario alla determinazione del portafoglio tangente e della CML.

Questo articolo è rivolto a un pubblico specifico: investitori evoluti, trader quantitativi, analisti finanziari e gestori sistematici. Si presuppone una certa familiarità con i concetti finanziari di base, ma l’esposizione sarà comunque strutturata per essere formativa e autoconsistente. L’obiettivo è fornire non solo la “ricetta” per la costruzione della frontiera efficiente, ma anche gli strumenti critici per interpretare i risultati, comprenderne i limiti e integrarli in un processo decisionale di investimento consapevole. Per chi opera con un approccio quantitativo, la padronanza di queste tecniche è un prerequisito essenziale, sia per lo sviluppo di strategie proprietarie sia per la valutazione di quelle altrui. Per i gestori, offre una metodologia scientifica per l’asset allocation strategica. Per l’investitore evoluto, rappresenta una chiave di lettura fondamentale per dialogare con i propri consulenti o per gestire in autonomia una parte del proprio patrimonio con maggiore cognizione di causa.

Nelle sezioni successive, intraprenderemo un viaggio dettagliato attraverso la teoria e la pratica della Frontiera Efficiente di Markowitz. Inizieremo con un inquadramento teorico-didattico, dove definiremo con precisione i concetti chiave, esploreremo le origini della MPT e discuteremo i suoi vantaggi e limiti intrinseci. Seguirà una sezione dedicata alla metodologia tecnica, in cui descriveremo il dataset utilizzato, la struttura logica dell’analisi (potenzialmente implementabile in Python, come suggerito nei materiali di studio), i criteri di calcolo e il funzionamento step-by-step del processo di ottimizzazione. Successivamente, ci tufferemo nell’analisi dei risultati, esaminando le visualizzazioni grafiche (la nuvola di portafogli simulati, la frontiera, MVP, Portafoglio Tangente, CML) e le metriche quantitative generate. Una sezione cruciale sarà dedicata all’interpretazione quantitativa di tali risultati, cercando di capire in quali contesti di mercato l’approccio funziona meglio, come può essere integrato operativamente e quali sono le riflessioni critiche da fare sui limiti del modello. Infine, nelle conclusioni e applicazioni, tireremo le somme su cosa questo studio dimostra, forniremo spunti operativi concreti, inclusi alcuni cenni all’integrazione con strategie in opzioni data la specializzazione di Kriterion Quant, e indicheremo come le risorse di Kriterion Quant possono supportare ulteriormente l’applicazione di queste conoscenze. Preparatevi a un’immersione completa in uno strumento che, nonostante i decenni trascorsi dalla sua introduzione, rimane di sconcertante attualità e potenza.

La rilevanza di questo studio per Kriterion Quant risiede nel suo duplice valore: educativo e pratico. Come piattaforma dedicata alla finanza quantitativa, Kriterion Quant mira a fornire ai propri utenti non solo strategie “black box”, ma soprattutto la comprensione profonda dei modelli sottostanti. Lo studio della Frontiera Efficiente di Markowitz è un esempio perfetto di questo approccio: un modello teoricamente elegante, ma con dirette implicazioni operative. Attraverso l’analisi che segue, i nostri lettori potranno apprezzare il rigore metodologico richiesto dalla finanza quantitativa e, al contempo, acquisire competenze direttamente spendibili nella gestione dei propri investimenti o nello sviluppo di strategie algoritmiche. L’obiettivo non è solo mostrare come si costruisce una frontiera efficiente, ma perché è importante e come interpretarla criticamente, in linea con la filosofia di Kriterion Quant di formare investitori consapevoli e preparati.

🟦 2. Inquadramento teorico-didattico

La Teoria Moderna di Portafoglio (MPT), introdotta da Harry Markowitz nel 1952 con il suo articolo “Portfolio Selection” pubblicato sul Journal of Finance, rappresenta una pietra miliare nella storia della finanza e della gestione degli investimenti. Prima di Markowitz, le decisioni di investimento erano spesso basate sulla valutazione dei singoli titoli, concentrandosi primariamente sul loro potenziale di rendimento e, in misura minore, sul rischio individuale. Markowitz ha rivoluzionato questo approccio dimostrando matematicamente che il rischio di un portafoglio non dipende solo dal rischio dei singoli asset che lo compongono, ma anche da come questi asset si muovono l’uno rispetto all’altro, ovvero dalla loro covarianza (o correlazione). Il concetto centrale è che la diversificazione, se attuata in modo intelligente, può ridurre il rischio complessivo del portafoglio senza necessariamente sacrificare il rendimento atteso. Lo studio che analizziamo si basa interamente su questi principi, mirando a costruire la “frontiera efficiente”: l’insieme di tutti i portafogli che offrono il massimo rendimento atteso per un determinato livello di rischio, o, equivalentemente, il minimo rischio per un determinato rendimento atteso. Ogni portafoglio che giace al di sotto di questa frontiera è sub-ottimale, poiché esiste un altro portafoglio sulla frontiera che offre un rendimento superiore a parità di rischio, o un rischio inferiore a parità di rendimento.

Le origini della MPT affondano nella teoria delle decisioni in condizioni di incertezza e nell’applicazione di metodi statistici ai mercati finanziari. Markowitz partì dall’assunzione che gli investitori sono, in generale, avversi al rischio: a parità di rendimento atteso, preferiscono il portafoglio con rischio minore. Inoltre, si assume che i rendimenti degli asset possano essere descritti da distribuzioni di probabilità, e che gli investitori basino le loro decisioni sui primi due momenti di queste distribuzioni: il valore atteso (media) dei rendimenti e la varianza (o deviazione standard) dei rendimenti come misura del rischio. Nonostante la MPT non incorpori direttamente aspetti comportamentali complessi, la sua logica contrasta alcune tendenze psicologiche comuni, come l’herding behavior (seguire la massa) o la concentration bias (eccessiva concentrazione su pochi titoli o settori, magari quelli più familiari o che hanno performato bene di recente). Dal punto di vista macroeconomico, la MPT non fa previsioni dirette, ma utilizza i dati storici dei rendimenti e delle loro interrelazioni (covarianze) per proiettare il comportamento futuro del portafoglio, assumendo una certa stazionarietà di queste relazioni, un’ipotesi che rappresenta uno dei suoi limiti più discussi. Tuttavia, il framework fornisce una disciplina quantitativa che aiuta a strutturare il processo di asset allocation.

Glossario Tecnico e Formule Utilizzate

Per comprendere appieno l’analisi della Frontiera Efficiente, è essenziale familiarizzare con alcuni termini tecnici e le relative formule. Di seguito, un glossario dei concetti chiave:

I vantaggi dell’approccio di Markowitz sono molteplici. Innanzitutto, fornisce un framework rigoroso e quantitativo per la costruzione di portafogli, spostando l’attenzione dalla selezione di singoli “vincitori” alla costruzione di un paniere ben bilanciato. In secondo luogo, enfatizza l’importanza della diversificazione e, soprattutto, del ruolo delle correlazioni tra asset. Permette di visualizzare chiaramente il trade-off tra rischio e rendimento, aiutando gli investitori a scegliere portafogli allineati con la propria propensione al rischio. L’identificazione del MVP e del Portafoglio Tangente offre punti di riferimento concreti per l’asset allocation.

🟦 3. Metodologia tecnica

L’implementazione pratica della Teoria Moderna di Portafoglio, finalizzata alla costruzione della Frontiera Efficiente, richiede un approccio metodologico rigoroso e ben definito. Questo studio, come delineato nei documenti forniti, segue una serie di passaggi logici, dall’acquisizione dei dati all’ottimizzazione e visualizzazione dei portafogli. La trasparenza metodologica è cruciale per interpretare correttamente i risultati e per replicare o estendere l’analisi. Esamineremo qui il dataset utilizzato, la struttura del codice che si presume sia stato impiegato (data la menzione di tool Python e l’orientamento pratico dello studio), i criteri di selezione impliciti ed espliciti, e il funzionamento dettagliato dell’algoritmo.

Il dataset utilizzato per questa analisi è un elemento cardine. I dati storici di prezzo sono stati raccolti per un insieme di 10 ticker azionari USA: Microsoft (MSFT), Apple (AAPL), Alphabet (GOOGL), Amazon (AMZN), Johnson & Johnson (JNJ), Visa (V), JPMorgan Chase (JPM), Procter & Gamble (PG), NVIDIA (NVDA) e Home Depot (HD). La fonte dei dati di prezzo, come indicato nelle preferenze generali di Kriterion Quant, è presumibilmente EODHD (End Of Day Historical Data) o una fonte equivalente che garantisca affidabilità e granularità. La frequenza dei dati è giornaliera, il che permette un’analisi sufficientemente dettagliata delle dinamiche di prezzo e delle correlazioni. L’intervallo temporale considerato per l’analisi storica si estende dal 1 Gennaio 2015 al 31 Dicembre 2024. Questo periodo di quasi dieci anni è significativo perché include diverse condizioni di mercato: fasi di bull market, correzioni, periodi di elevata volatilità (come l’inizio della pandemia COVID-19) e differenti regimi di tassi d’interesse. Tale varietà contribuisce a rendere le stime di rendimento, volatilità e covarianza più rappresentative di un ciclo economico completo, sebbene non esenti dalle limitazioni dell’estrapolazione storica. Per l’annualizzazione dei rendimenti e della volatilità, si è utilizzato un valore standard di 252 giorni di trading annuali. Parallelamente, per i calcoli che richiedono un tasso privo di rischio (come lo Sharpe Ratio e la Capital Market Line), è stato impiegato un tasso risk-free del 2.09% annualizzato. Questo valore è stato derivato dalla media dei rendimenti del Treasury Bill a 3 mesi (simbolo ^IRX) nello stesso periodo 2015-2024, garantendo coerenza temporale con i dati degli asset rischiosi.

La struttura del codice utilizzato per realizzare uno studio di questo tipo, specialmente in un contesto orientato alla finanza quantitativa come Kriterion Quant, si basa tipicamente su Python e le sue librerie scientifiche (NumPy, Pandas, SciPy, Matplotlib/Plotly). Il “Testo didattico” fornito delinea un flusso logico che può essere tradotto in uno pseudocodice o in una sequenza di operazioni. Sebbene il codice sorgente specifico non sia fornito integralmente, possiamo inferirne la struttura:

Pseudocodice / Flusso Logico dell’Analisi:

// Fase 1: Acquisizione e Preparazione dei Dati
1.  DEFINIRE la lista dei ticker azionari (MSFT, AAPL, ..., HD).
2.  DEFINIRE il periodo di analisi (01/01/2015 - 31/12/2024).
3.  SCARICARE i dati storici dei prezzi di chiusura giornalieri per i ticker selezionati (da EODHD o simile).
4.  PULIRE e PREPARARE i dati (gestire valori mancanti, allineare le serie storiche).
5.  CALCOLARE i rendimenti giornalieri (logaritmici o semplici) per ogni asset.
// Rendimento semplice: (Prezzo_t / Prezzo_t-1) - 1
    // Rendimento logaritmico: ln(Prezzo_t / Prezzo_t-1)

// Fase 2: Calcolo delle Statistiche di Base degli Asset
6.  CALCOLARE il rendimento medio giornaliero per ogni asset.
7.  ANNUALIZZARE il rendimento medio (moltiplicando per 252).
8.  CALCOLARE la matrice di covarianza dei rendimenti giornalieri.
9.  ANNUALIZZARE la matrice di covarianza (moltiplicando per 252).
10. CALCOLARE la volatilità annualizzata per ogni asset (radice quadrata della diagonale della matrice di covarianza annualizzata).
// Fase 3: Simulazione Monte Carlo di Portafogli Casuali
11. DEFINIRE il numero di simulazioni (es. 20.000 come menzionato nella "Scheda Tecnica").
12. INIZIALIZZARE array per salvare pesi, rendimenti, volatilità e Sharpe Ratio dei portafogli simulati.
13. PER ogni simulazione (da 1 a 20.000):
    a. GENERARE un set di pesi casuali per gli asset (somma dei pesi = 1, pesi individuali tra 0 e 1, no short selling).
    b. CALCOLARE il rendimento atteso del portafoglio simulato (usando i pesi e i rendimenti medi annualizzati degli asset).
    c. CALCOLARE la volatilità del portafoglio simulato (usando i pesi e la matrice di covarianza annualizzata).
    d. CALCOLARE lo Sharpe Ratio del portafoglio simulato (usando il tasso risk-free del 2.09%).
    e. SALVARE pesi, rendimento, volatilità e Sharpe Ratio.

// Fase 4: Ottimizzazione per Portafogli Chiave
14. OTTIMIZZAZIONE PER IL PORTAFOGLIO A VARIANZA MINIMA (MVP):
    a. DEFINIRE la funzione obiettivo: minimizzare la volatilità del portafoglio.
    b. DEFINIRE i vincoli: somma dei pesi = 1 ( {'type': 'eq', 'fun': lambda weights: np.sum(weights) - 1} ), pesi individuali tra 0 e 1 (bounds = (0,1) for each asset).
    c. Eseguire l'ottimizzazione (es. usando `scipy.optimize.minimize` con metodo SLSQP).
    d. CALCOLARE rendimento e volatilità del MVP.
15. OTTIMIZZAZIONE PER IL PORTAFOGLIO TANGENTE (MAX SHARPE RATIO):
    a. DEFINIRE la funzione obiettivo: massimizzare lo Sharpe Ratio (o minimizzare il negativo dello Sharpe Ratio).
    b. DEFINIRE i vincoli: somma dei pesi = 1, pesi individuali tra 0 e 1.
    c. Eseguire l'ottimizzazione.
    d. CALCOLARE rendimento, volatilità e Sharpe Ratio del Portafoglio Tangente.
// Fase 5: Costruzione della Frontiera Efficiente (tramite ottimizzazione)
16. DEFINIRE un range di rendimenti target (es. dal rendimento del MVP a un rendimento massimo osservato o desiderato).
17. PER ogni rendimento target nel range:
    a. OTTIMIZZARE per trovare il portafoglio che minimizza la volatilità per quel rendimento target.
// Vincoli: somma dei pesi = 1, pesi individuali tra 0 e 1, rendimento del portafoglio = rendimento target.
    b. SALVARE la volatilità e il rendimento del portafoglio sulla frontiera.
// Fase 6: Visualizzazione e Reporting (come da "Markowitz_Efficient_Frontier_Report_Improved.html")
18. PLOTTARE:
    a. I portafogli simulati (nuvola di punti rischio-rendimento, colorati per Sharpe Ratio).
    b. La Frontiera Efficiente (la curva dei portafogli ottimizzati).
    c. Il Portafoglio a Varianza Minima (MVP) – evidenziato.
    d. Il Portafoglio Tangente (Max Sharpe Ratio) – evidenziato.
    e. La Capital Market Line (CML) – la retta dal risk-free rate attraverso il Portafoglio Tangente.
19. GENERARE un report (es. HTML con Jinja2) che includa i grafici, le tabelle con le composizioni dei portafogli chiave (MVP, Tangente), e le statistiche rilevanti.

I criteri di selezione degli asset sono principalmente basati sulla loro appartenenza a un paniere di titoli noti e liquidi del mercato USA. Non vengono menzionati filtri quantitativi specifici (es. momentum, value) per la pre-selezione dei 10 ticker; la selezione sembra essere discrezionale, finalizzata a creare un universo di investimento diversificato per settore e rappresentativo. Per quanto riguarda i vincoli di ottimizzazione, la “Scheda Tecnica” è esplicita:

• Somma dei Pesi: La somma dei pesi di tutti gli asset in un portafoglio deve essere uguale a 1. Questo è un vincolo standard che assicura che tutto il capitale sia allocato. Matematicamente: {‘type’: ‘eq’, ‘fun’: lambda weights: np.sum(weights) – 1}.
• Pesi Individuali (Bound): Si assume l’assenza di short selling, quindi i pesi per ogni asset sono vincolati tra 0 e 1 ((0, 1) per ogni asset). Questo significa che non è possibile vendere allo scoperto un titolo e che l’investimento massimo in un singolo titolo non può eccedere il 100% del portafoglio (anche se quest’ultimo è implicitamente gestito dalla somma dei pesi a 1). Questi vincoli sono comuni nella pratica per molti investitori e fondi.

Il funzionamento dell’algoritmo step-by-step è stato delineato nello pseudocodice. Fondamentalmente, si parte dai rendimenti storici per stimare i parametri futuri attesi (medie, varianze, covarianze). La simulazione Monte Carlo gioca un ruolo esplorativo: generando migliaia di portafogli con pesi casuali, si ottiene una “nuvola” di possibili combinazioni rischio/rendimento, che dà una prima idea della forma della regione ammissibile. Tuttavia, per identificare con precisione la frontiera e i portafogli chiave, si ricorre a tecniche di ottimizzazione numerica (come Sequential Least Squares Programming – SLSQP, un metodo adatto per problemi con vincoli non lineari). L’ottimizzatore cerca attivamente i pesi che soddisfano i vincoli imposti (somma a 1, no short selling) e che, contemporaneamente, minimizzano una funzione obiettivo (la volatilità per il MVP e per i punti della frontiera, o il negativo dello Sharpe Ratio per il Portafoglio Tangente). La costruzione della frontiera efficiente “vera e propria” avviene iterando l’ottimizzazione per diversi livelli di rendimento target, trovando per ciascuno il portafoglio con la minima volatilità. Questo approccio è più preciso della semplice interpolazione dei risultati della Monte Carlo. Infine, la CML viene tracciata analiticamente una volta identificato il Portafoglio Tangente e noto il tasso risk-free. L’intero processo è computazionalmente intensivo ma gestibile con hardware moderno e software ottimizzato.

🟦 4. Analisi dei Risultati

L’applicazione della metodologia descritta a un portafoglio composto dai 10 ticker azionari USA selezionati (MSFT, AAPL, GOOGL, AMZN, JNJ, V, JPM, PG, NVDA, HD) e utilizzando un tasso risk-free del 2.09% su dati dal 2015 al 2024, genera una serie di output quantitativi e grafici che sono al cuore dello studio sulla Frontiera Efficiente di Markowitz. Questi risultati permettono di visualizzare e quantificare il trade-off rischio/rendimento e di identificare portafogli teoricamente ottimali. L’analisi si basa, come indicato, sulla simulazione di 20.000 portafogli con pesi casuali e sull’ottimizzazione numerica per affinare la frontiera e individuare i portafogli specifici.

I principali risultati generati dallo studio includono:

• Una nuvola di 20.000 portafogli simulati, ciascuno rappresentato da un punto nel piano rischio (volatilità) – rendimento. Questi punti illustrano l’universo delle possibili combinazioni ottenibili con gli asset dati e i vincoli imposti.
• La Frontiera Efficiente, ovvero la curva che delimita superiormente la nuvola dei portafogli simulati. Ogni punto su questa curva rappresenta un portafoglio che offre il massimo rendimento atteso per un dato livello di rischio.
• Il Portafoglio a Varianza Minima (MVP), identificato come il punto più a sinistra sulla Frontiera Efficiente, corrispondente al portafoglio con la volatilità più bassa in assoluto.
• Il Portafoglio Tangente (o Portafoglio Max Sharpe Ratio), identificato come il portafoglio sulla Frontiera Efficiente che massimizza lo Sharpe Ratio. Questo portafoglio è cruciale perché rappresenta l’allocazione ottimale tra gli asset rischiosi quando si considera la possibilità di investire o prendere a prestito al tasso risk-free.
• La Capital Market Line (CML), una linea retta che parte dal tasso risk-free sull’asse dei rendimenti e passa per il Portafoglio Tangente. La CML rappresenta i portafogli più efficienti che si possono ottenere combinando il Portafoglio Tangente con l’asset privo di rischio.
• Le composizioni (pesi) dei portafogli chiave (MVP e Portafoglio Tangente), che indicano la percentuale di capitale da allocare a ciascuno dei 10 ticker per ottenere tali portafogli.
• Le metriche di performance e rischio (rendimento atteso, volatilità, Sharpe Ratio) per i portafogli chiave.

Spiegazione dei Grafici Inclusi nei Report

“Grafico 5.1: Portafogli Simulati con il metodo Monte Carlo, visualizzati per Rischio (Volatilità), Rendimento Atteso Annualizzato e Sharpe Ratio. Sono indicati il Portafoglio a Varianza Minima Globale (GMV) e il Portafoglio con Massimo Sharpe Ratio (MSR).”

Descrizione del Grafico: Questo è il grafico principale dello studio. L’asse X rappresenta la volatilità annualizzata (rischio), mentre l’asse Y rappresenta il rendimento atteso annualizzato.

• Nuvola di Punti (Portafogli Simulati): Ogni punto rappresenta uno dei 20.000 portafogli generati casualmente. I punti sono spesso colorati in base al loro Sharpe Ratio, permettendo di identificare visivamente le aree con migliori performance aggiustate per il rischio (tipicamente i punti più in alto e a sinistra, tendenti alla frontiera).
• Frontiera Efficiente: È una curva continua che si trova sopra la nuvola di punti. Rappresenta i portafogli che sono “efficienti” secondo Markowitz. Qualsiasi portafoglio al di sotto di questa curva è sub-ottimale.
• Portafoglio a Varianza Minima (MVP): Un punto specifico sulla Frontiera Efficiente, marcato solitamente con un simbolo distintivo (es. una stella o un cerchio di colore diverso). È il punto della frontiera con la minima volatilità (il più a sinistra).
• Portafoglio Tangente (Max Sharpe Ratio): Un altro punto specifico sulla Frontiera Efficiente, anch’esso marcato. È il punto in cui una linea retta (la CML) partendo dal tasso risk-free sull’asse Y è tangente alla Frontiera Efficiente. Questo portafoglio ha lo Sharpe Ratio più elevato tra tutti i portafogli composti solo da asset rischiosi.
• Capital Market Line (CML): Una linea retta che parte dal valore del tasso risk-free (2.09% in questo studio) sull’asse Y (volatilità zero) e passa attraverso il Portafoglio Tangente, estendendosi verso l’alto e verso destra. I portafogli sulla CML sono combinazioni del Portafoglio Tangente e dell’asset privo di rischio.

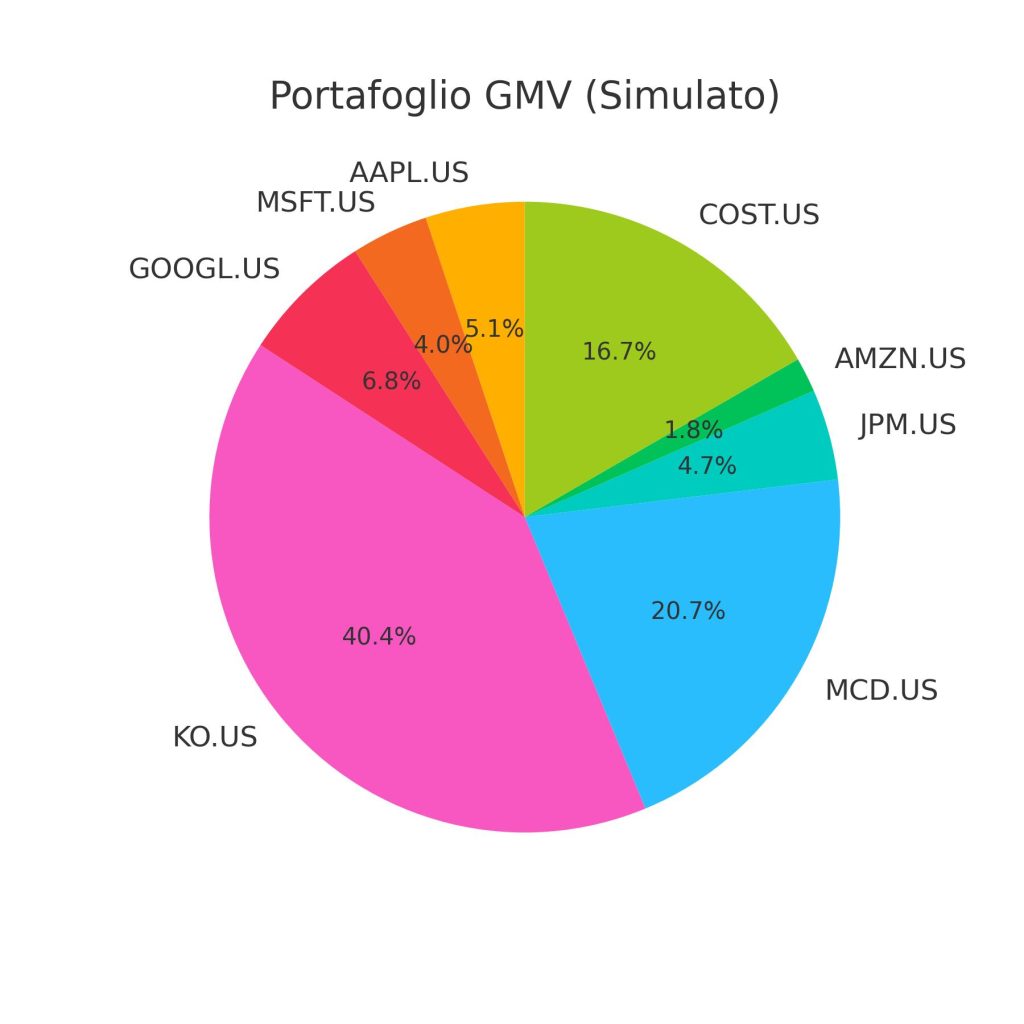
“Figura 1: Ripartizione percentuale degli asset all’interno del Portafoglio a Varianza Minima Globale (GMV) simulato.”

Descrizione del Grafico: Questo grafico visualizza i pesi percentuali di ciascuno dei 10 ticker (MSFT, AAPL, …, HD) all’interno del Portafoglio a Varianza Minima. Aiuta a comprendere quali asset contribuiscono maggiormente alla minimizzazione del rischio e l’effettivo livello di diversificazione raggiunto.

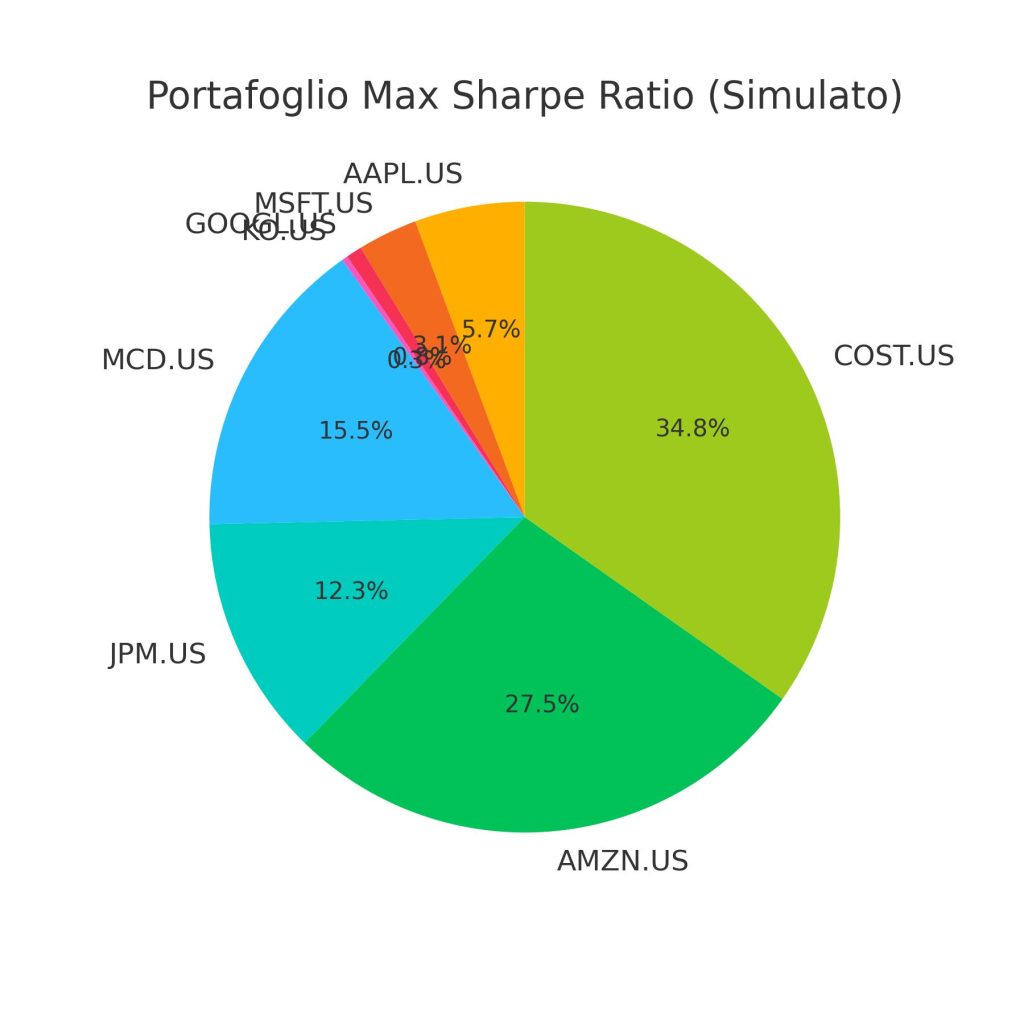
“Figura 2: Ripartizione percentuale degli asset all’interno del Portafoglio per il Massimo Sharpe Ratio (MSR) simulato.”

Descrizione del Grafico: Simile al precedente, ma mostra i pesi percentuali dei 10 ticker che costituiscono il Portafoglio Tangente. È interessante confrontare questa composizione con quella del MVP per vedere come cambiano le allocazioni quando l’obiettivo diventa massimizzare il rendimento aggiustato per il rischio.

Tabella con le Metriche Analizzate

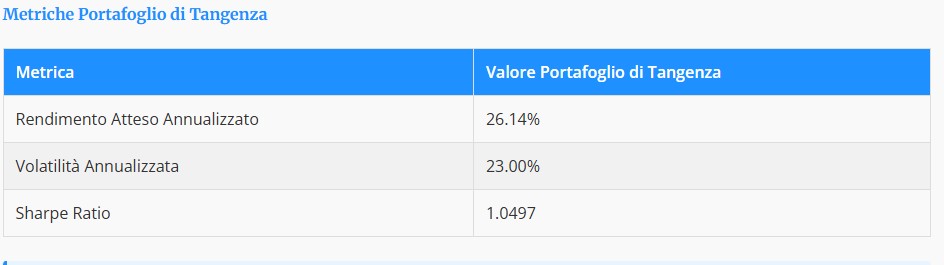
“Tabella 1: Riepilogo delle metriche chiave – Rendimento Atteso Annualizzato, Volatilità Annualizzata e Sharpe Ratio – per il Portafoglio di Tangenza.”

La tabella visualizzata, denominata ‘Metriche Portafoglio di Tangenza’, offre un quadro sintetico delle performance attese e del profilo di rischio associati a un Portafoglio di Tangenza specifico. Questi dati sono fondamentali per gli investitori e gli analisti per valutare l’attrattiva e l’efficienza di tale strategia di investimento.

Nello specifico, i valori chiave presentati nella tabella sono:

• Rendimento Atteso Annualizzato: Questo valore, pari al 26.14%, rappresenta la stima del ritorno percentuale che il portafoglio potrebbe generare su base annua.
• Volatilità Annualizzata: Fissata al 23.00%, questa metrica quantifica il grado di dispersione dei rendimenti del portafoglio attorno alla sua media attesa, fungendo da indicatore principale del suo rischio.
• Sharpe Ratio: Calcolato a 1.0497, questo indice misura il rendimento del portafoglio al netto del tasso privo di rischio, per unità di rischio (volatilità). Un valore superiore a 1, come in questo caso, è generalmente indicativo di una buona performance aggiustata per il rischio.

Insieme, queste tre metriche forniscono una valutazione concisa ma potente delle caratteristiche del Portafoglio di Tangenza, consentendo un confronto informato con altre opportunità di investimento o benchmark di riferimento.

Confronto con Buy&Hold o Altre Metriche Standard

La Teoria Moderna di Portafoglio offre un framework per l’allocazione ex-ante. Un confronto diretto con una strategia di Buy & Hold (B&H) su un singolo asset o su un indice di riferimento (come l’S&P 500, sebbene non esplicitamente parte dei ticker analizzati come benchmark unico) richiederebbe un backtest storico delle performance dei portafogli ottimizzati (MVP e Tangente), con ribilanciamenti periodici per mantenere i pesi target. I documenti forniti si concentrano sulla costruzione statica della frontiera basata su dati storici complessivi, piuttosto che su un backtest dinamico.

Tuttavia, possiamo ipotizzare un confronto concettuale. Una strategia B&H su un singolo titolo (es. solo MSFT) avrebbe il rendimento e la volatilità storica di MSFT. Una strategia B&H su un portafoglio equiponderato dei 10 ticker avrebbe un suo specifico profilo rischio/rendimento, che probabilmente si collocherebbe da qualche parte all’interno della nuvola dei portafogli simulati, ma difficilmente sulla frontiera efficiente.

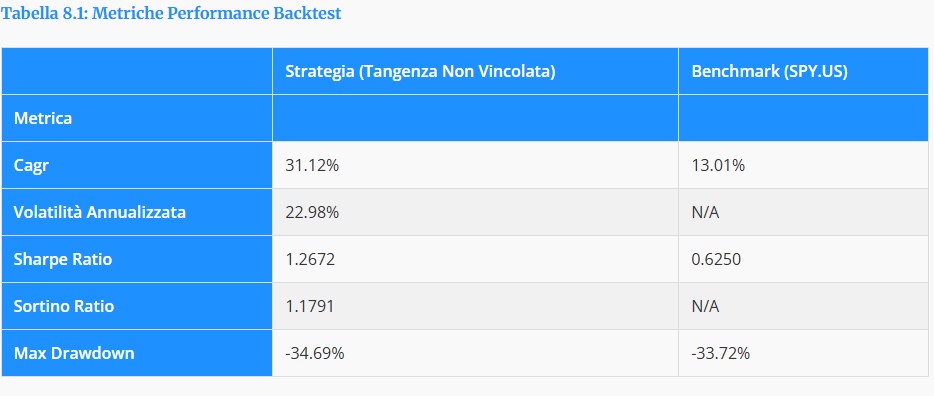
“Tabella 8.1: Riepilogo delle metriche di performance del backtest, a confronto tra la ‘Strategia (Tangenza Non Vincolata)’ e il benchmark di mercato ‘SPY.US’.”

La ‘Tabella 8.1: Metriche Performance Backtest’ offre un’analisi comparativa essenziale per valutare l’efficacia di una ‘Strategia (Tangenza Non Vincolata)’ rispetto all’investimento passivo nel benchmark ‘SPY.US’. I risultati del backtest sono riassunti attraverso metriche standard del settore:

Il Cagr evidenzia un tasso di crescita annuo composto del 31.12% per la strategia, notevolmente più alto del 13.01% ottenuto dal benchmark. La Volatilità Annualizzata della strategia si attesta al 22.98% (dato non fornito per il benchmark).

In termini di rendimento aggiustato per il rischio, lo Sharpe Ratio della strategia (1.2672) è circa il doppio di quello del benchmark (0.6250). Similmente, il Sortino Ratio, che considera solo la volatilità negativa, è di 1.1791 per la strategia (N/A per il benchmark).

Riguardo al rischio di perdita massima, il Max Drawdown della strategia è stato del -34.69%, leggermente più accentuato rispetto al -33.72% del benchmark. Questa analisi suggerisce una potenziale sovraperformance della strategia in termini di crescita e di efficienza del capitale, a fronte di un’esposizione al ribasso massima paragonabile a quella del mercato.

🟦 5. Interpretazione quantitativa

L’analisi dei risultati della Frontiera Efficiente di Markowitz, pur essendo un esercizio teoricamente solido, acquisisce pieno valore solo attraverso una corretta interpretazione quantitativa e contestualizzata. Comprendere le condizioni in cui il modello tende a performare meglio, come integrare operativamente questi concetti in portafogli reali, e riconoscere i limiti intrinseci del modello sono passaggi fondamentali per un utilizzo consapevole e proficuo. Questa sezione si propone di esplorare tali aspetti, fornendo una lettura critica e pragmatica dei risultati ottenuti.

Il modello di Markowitz, e quindi la Frontiera Efficiente, tende a funzionare meglio o a fornire indicazioni più affidabili in determinate condizioni di mercato e per specifici orizzonti temporali. Generalmente, l’approccio è più indicato per allocazioni strategiche di lungo periodo piuttosto che per decisioni tattiche di breve termine. Questo perché le stime di rendimenti attesi, volatilità e correlazioni, basate su dati storici, tendono ad avere una maggiore stabilità e predittività su orizzonti pluriennali. In periodi di mercato relativamente stabili o con trend direzionali chiari, dove le relazioni storiche tra asset (correlazioni) mantengono una certa persistenza, la frontiera calcolata può offrire una buona approssimazione dei portafogli ottimali. Al contrario, durante fasi di forte stress di mercato, crisi sistemiche o cambi di regime macroeconomico, le correlazioni tra asset possono convergere rapidamente verso 1 (tutti gli asset scendono insieme), riducendo drasticamente i benefici della diversificazione così come modellati dalla MPT tradizionale e rendendo le stime storiche meno rilevanti. Inoltre, il modello performa meglio quando gli asset considerati hanno distribuzioni dei rendimenti che non si discostano eccessivamente dalla normalità o, quantomeno, quando le deviazioni (come code pesanti o forte asimmetria) sono comprese e gestite con cautela. L’efficacia dipende anche dalla qualità e rappresentatività dei dati di input: serie storiche lunghe e affidabili, che coprono diversi cicli economici, sono preferibili.

L’integrazione operativa dei concetti della Frontiera Efficiente può variare significativamente a seconda del profilo dell’investitore:

• Investitore Retail Evoluto: Per un investitore privato con buone conoscenze finanziarie, la Frontiera Efficiente può servire come guida per l’asset allocation strategica del proprio portafoglio di lungo termine. Dopo aver definito la propria tolleranza al rischio, l’investitore può identificare un punto sulla frontiera (o sulla CML se si include il risk-free) che corrisponde al livello di rischio desiderato e osservare la composizione del portafoglio ottimale suggerita. Può essere uno strumento per evitare un’eccessiva concentrazione su pochi titoli “preferiti” e per apprezzare i benefici di includere asset meno correlati. Ad esempio, se l’analisi mostra che il Portafoglio Tangente ha un buon Sharpe Ratio, l’investitore potrebbe cercare di replicarne la struttura tramite ETF o singoli titoli, ribilanciando periodicamente (es. annualmente) per mantenere le allocazioni target.
• Gestore di Portafoglio: I gestori possono utilizzare la MPT come base per la costruzione di portafogli modello o come benchmark per valutare l’efficienza delle proprie allocazioni attive. L’ottimizzazione di Markowitz può essere il punto di partenza, a cui poi aggiungere view tattiche, vincoli specifici del mandato (es. limiti settoriali, tracking error), o integrare fattori di rischio alternativi. Ad esempio, un gestore potrebbe utilizzare la MPT per definire l’allocazione strategica tra diverse asset class (azioni, obbligazioni, materie prime, ecc.) e poi sovra/sottopesare tatticamente in base alle proprie previsioni di mercato.
• Trader Sistematico/Quant: Per i trader sistematici, la MPT può essere uno dei moduli all’interno di strategie più complesse. Ad esempio, una strategia di rotazione settoriale potrebbe utilizzare un’ottimizzazione di Markowitz per allocare il capitale tra i settori selezionati in un dato momento. Oppure, i concetti di rischio di portafoglio e correlazione sono fondamentali nello sviluppo di strategie market-neutral o di pair trading. Il trader quantitativo è anche colui che più probabilmente esplorerà le estensioni della MPT, come l’ottimizzazione di Black-Litterman (che permette di integrare le view dell’investitore con le stime di mercato) o l’utilizzo di stimatori più robusti per la matrice di covarianza.

Esistono diverse strategie che possono derivare o essere informate dall’analisi della Frontiera Efficiente. Le strategie calendar-based, come il ribilanciamento annuale o semestrale ai pesi del Portafoglio Tangente o di un altro portafoglio target sulla frontiera, sono un’applicazione diretta. Le strategie di overlay potrebbero utilizzare derivati (come opzioni o futures) per modificare il profilo rischio/rendimento di un portafoglio ottimizzato secondo Markowitz, ad esempio per proteggerlo da ribassi (protective put) o per generare extra reddito (covered call) senza alterare drasticamente l’allocazione strategica sottostante. Le strategie di rotazione possono selezionare dinamicamente un sottoinsieme di asset dall’universo di investimento e poi applicare l’ottimizzazione di Markowitz a questo sottoinsieme, aggiornando periodicamente la selezione e l’allocazione. Ad esempio, si potrebbe combinare un filtro di momentum sui 10 ticker e poi ottimizzare un portafoglio solo con i 5 migliori.

Per affrontare alcuni di questi limiti e migliorare la robustezza dell’analisi, si possono esplorare diversi miglioramenti futuri, come suggerito anche nel documento “Analisi Quantitativa”:

• Validazioni Rolling (Walk-Forward Optimization): Invece di ottimizzare sull’intero periodo storico in un’unica soluzione, si può effettuare l’ottimizzazione su una finestra mobile di dati (es. gli ultimi 3-5 anni) e poi testare la performance del portafoglio risultante sul periodo successivo (out-of-sample). Questo processo viene ripetuto iterativamente, fornendo una misura più realistica della performance storica effettiva di una strategia basata sulla MPT.
• Cross-Asset Validation: Applicare la metodologia a diversi universi di asset (es. azioni europee, mercati emergenti, diverse asset class come obbligazionario, commodities) per testarne la generalizzabilità.
• Utilizzo di Stimatori Robusti: Impiegare tecniche statistiche più avanzate per stimare la matrice di varianza-covarianza (es. shrinkage estimators come Ledoit-Wolf, o modelli fattoriali) che possono portare a stime più stabili e meno soggette a errori di campionamento.
• Integrazione di Filtri Tecnici o Fondamentali: Combinare l’ottimizzazione di Markowitz con segnali provenienti da altri indicatori (es. medie mobili, RSI, P/E ratio) per la selezione degli asset o per temporizzare gli investimenti.
• Implementazioni Logiche Avanzate: Considerare modelli di ottimizzazione più sofisticati, come l’ottimizzazione robusta (che tiene conto dell’incertezza negli input), l’ottimizzazione multi-obiettivo (es. massimizzare il rendimento e minimizzare il drawdown massimo contemporaneamente), o l’integrazione di vincoli più complessi (es. limiti di turnover, requisiti di liquidità). Come accennato nell’analisi fornita, anche l’integrazione di strategie opzionali potrebbe essere un’area di sviluppo per modellare e gestire il profilo di rischio/rendimento in modo più granulare.

In sintesi, l’interpretazione quantitativa della Frontiera Efficiente non deve essere un atto di fede cieca nei confronti del modello, ma un processo critico che ne riconosce la potenza come strumento di diversificazione e gestione del rischio, pur essendo consapevole delle sue ipotesi e dei suoi limiti. La vera abilità sta nell’adattare il framework teorico al contesto specifico e agli obiettivi dell’investitore.

🟦 6. Conclusioni e Applicazioni

Lo studio della Frontiera Efficiente di Markowitz, come abbiamo esplorato nelle sezioni precedenti analizzando un portafoglio di 10 importanti titoli azionari USA nel periodo 2015-2024, dimostra in modo inequivocabile il valore intrinseco della diversificazione scientifica e l’importanza di un approccio quantitativo alla gestione del portafoglio. Non si tratta di una novità assoluta, essendo la Teoria Moderna di Portafoglio (MPT) un caposaldo della finanza da oltre settant’anni, ma la sua applicazione pratica e la sua comprensione rimangono di fondamentale rilevanza per chiunque operi sui mercati finanziari con serietà e metodo. Questo studio ribadisce che, attraverso un’attenta analisi dei rendimenti attesi, delle volatilità e, soprattutto, delle correlazioni tra gli asset, è possibile costruire portafogli che offrono un profilo rischio/rendimento superiore rispetto a scelte basate sull’istinto o sulla selezione di singoli titoli isolati. La visualizzazione della “nuvola” di portafogli, della frontiera che la sovrasta, e l’identificazione di portafogli chiave come il Portafoglio a Varianza Minima (MVP) e il Portafoglio Tangente (Max Sharpe Ratio) forniscono una mappa concreta per navigare le decisioni di investimento.

L’oggetto dello studio, la MPT e la costruzione della frontiera efficiente, andrebbe utilizzato principalmente come framework per l’asset allocation strategica di medio-lungo periodo. È uno strumento potente quando si definisce la struttura portante di un portafoglio, specialmente se si dispone di un universo di investimento sufficientemente ampio e diversificato. È particolarmente utile per gli investitori che hanno una chiara definizione della propria tolleranza al rischio e cercano di massimizzare il rendimento atteso per quel dato livello di rischio (o viceversa). La sua applicazione è logica quando si crede che le relazioni storiche tra asset (in particolare le correlazioni) abbiano una qualche persistenza nel tempo, o quando si utilizzano stimatori robusti per questi parametri. Andrebbe, invece, evitato o usato con estrema cautela come unico strumento per decisioni di trading di breve termine o per market timing stretto. La sensibilità del modello agli input, soprattutto ai rendimenti attesi che sono notoriamente difficili da prevedere, e la sua tendenza a produrre risultati instabili se basato su periodi storici brevi o atipici, lo rendono meno adatto a contesti altamente dinamici e speculativi se non integrato con altri segnali o modelli. Inoltre, in periodi di panico di mercato, quando le correlazioni tendono a uno e la diversificazione tradizionale fallisce temporaneamente, la frontiera efficiente calcolata su dati “normali” perde gran parte della sua rilevanza immediata, sebbene possa rimanere una guida per la ricostruzione del portafoglio una volta che la tempesta è passata.

Integrare la Frontiera Efficiente in un framework operativo richiede disciplina e consapevolezza dei suoi limiti. Un approccio pragmatico potrebbe includere i seguenti passaggi:

1. Definizione dell’Universo Investibile: Selezionare attentamente gli asset o le asset class da includere nell’analisi, considerando liquidità, disponibilità di dati e coerenza con gli obiettivi di investimento.
2. Stima degli Input: Utilizzare dati storici sufficientemente lunghi e, se possibile, tecniche di stima robuste (es. shrinkage per le covarianze, modelli fattoriali per i rendimenti attesi o l’approccio di Black-Litterman per incorporare view soggettive). Essere consapevoli dell’incertezza di queste stime.
3. Costruzione della Frontiera e Identificazione dei Portafogli Chiave: Eseguire l’ottimizzazione con vincoli realistici (es. no short selling, limiti di concentrazione per singolo titolo/settore).
4. Selezione del Portafoglio Target: Scegliere un portafoglio sulla frontiera (o sulla CML) che sia allineato con la propria propensione al rischio e gli obiettivi di rendimento.
5. Implementazione e Ribilanciamento: Attuare il portafoglio e definire una politica di ribilanciamento (es. basata su soglie di deviazione dei pesi o su base temporale, come annuale) per mantenere l’allocazione desiderata, tenendo conto dei costi di transazione.
6. Monitoraggio e Revisione: Rivedere periodicamente (es. annualmente o in caso di cambiamenti significativi del mercato o degli obiettivi personali) le stime degli input e l’adeguatezza del portafoglio target.

Considerando la specializzazione di Kriterion Quant, è interessante esplorare spunti operativi relativi alle Opzioni in questo contesto. Sebbene la MPT classica non tratti direttamente le opzioni (che hanno distribuzioni dei rendimenti fortemente asimmetriche), queste possono essere integrate in modo strategico:

• Overlay Protettivi: Un portafoglio ottimizzato secondo Markowitz (es. il Portafoglio Tangente) può essere protetto da crolli di mercato acquistando opzioni put sull’indice di riferimento o sui singoli componenti più rischiosi. Questo altera il profilo rischio/rendimento, introducendo un “pavimento” alla perdita massima, al costo del premio pagato per le opzioni.
• Generazione di Reddito (Covered Call): Sui singoli titoli che compongono un portafoglio ottimizzato, si potrebbero vendere opzioni call coperte (covered call) per generare un extra rendimento (il premio incassato). Questo approccio limita il potenziale di upside del singolo titolo ma può migliorare il rendimento complessivo in mercati laterali o moderatamente rialzisti, e può anche ridurre leggermente la volatilità del portafoglio.
• Modellazione del Rischio Avanzata: Per portafogli che includono strutturalmente strategie opzionali complesse (es. credit spread, iron condor), la MPT tradizionale basata solo su media e varianza è insufficiente. Qui si entra nel campo di modelli di portafoglio più avanzati che possono gestire distribuzioni non normali e payoff non lineari, ma la comprensione della MPT rimane un prerequisito.
• Esposizione Sintetica: Le opzioni possono essere utilizzate per replicare sinteticamente l’esposizione a determinati asset del portafoglio ottimale, magari in modo più efficiente dal punto di vista del capitale o per gestire vincoli specifici.

Questo studio sulla Frontiera Efficiente di Markowitz è solo un esempio del tipo di analisi rigorosa e applicata che Kriterion Quant si impegna a fornire. La finanza quantitativa è un campo vasto e in continua evoluzione, e la padronanza di strumenti come la MPT è essenziale per navigarlo con successo.

Sei pronto ad approfondire e a mettere in pratica queste conoscenze?

Kriterion Quant offre diverse risorse per accompagnarti nel tuo percorso:

Non lasciare che la complessità dei mercati ti intimidisca. Con gli strumenti giusti e una solida preparazione, puoi trasformare l’incertezza in opportunità. Contattaci per discutere di come Kriterion Quant può supportare i tuoi obiettivi di investimento e di apprendimento nella finanza quantitativa.

In conclusione, la Frontiera Efficiente di Markowitz non è una formula magica, ma un potente faro che illumina il cammino verso decisioni di investimento più razionali e scientificamente fondate. La sua comprensione, applicazione e, soprattutto, la sua interpretazione critica sono competenze che ogni investitore evoluto, quant e gestore sistematico dovrebbe aspirare a padroneggiare. E Kriterion Quant è qui per guidarti in questo percorso.

Disclaimer e Avvertenze

Il presente studio sull’analisi della stagionalità del titolo Apple Inc. (AAPL.US) è fornito esclusivamente a scopo informativo, educativo e di ricerca. Le informazioni, le analisi, i dati e le opinioni qui contenuti non costituiscono in alcun modo una consulenza finanziaria, una raccomandazione di investimento, un’offerta o una sollecitazione all’acquisto o alla vendita di strumenti finanziari.
Nessuna Garanzia di Accuratezza o Completezza: Sebbene sia stato fatto ogni sforzo per garantire l’accuratezza e la completezza delle informazioni presentate, basate su fonti dati ritenute affidabili (EODHD per i dati di prezzo storici e analisi Python interne), non viene fornita alcuna garanzia esplicita o implicita in tal senso. Errori nei dati, nella metodologia o nell’interpretazione sono possibili.

La Performance Passata Non È Indicativa di Risultati Futuri: I risultati storici, i pattern stagionali, le performance dei backtest e qualsiasi altra analisi retrospettiva presentata in questo documento non sono in alcun modo una garanzia né un’indicazione affidabile di risultati futuri. I mercati finanziari sono intrinsecamente volatili e influenzati da una moltitudine di fattori imprevedibili. I pattern osservati nel passato potrebbero non persistere nel futuro.
Rischio di Perdita: Qualsiasi decisione di investimento o di trading basata sulle informazioni contenute in questo studio è presa a totale ed esclusivo rischio dell’investitore. L’investimento in strumenti finanziari, inclusi titoli azionari come AAPL.US, comporta un rischio significativo di perdita del capitale investito, che può arrivare fino alla perdita totale.
Non Personalizzazione: Questo studio ha carattere generale e non tiene conto degli obiettivi di investimento specifici, della situazione finanziaria, della propensione al rischio o delle esigenze particolari di alcun individuo o entità. Prima di prendere qualsiasi decisione di investimento, è fondamentale consultare un consulente finanziario qualificato e indipendente che possa valutare l’adeguatezza di qualsiasi strategia o strumento finanziario alla luce della situazione personale dell’investitore.
Costi di Transazione e Tasse: Le analisi e i backtest presentati potrebbero non aver tenuto conto dei costi di transazione (commissioni, spread, slippage) né delle implicazioni fiscali, che possono influenzare significativamente i rendimenti netti effettivi.
Limiti dei Backtest: I backtest sono simulazioni di strategie passate e sono soggetti a limitazioni, inclusa la possibilità di sovra-ottimizzazione (data-mining bias) e il fatto che vengono eseguiti con il senno di poi. Non riflettono l’impatto di fattori di mercato reali come la liquidità e lo stress emotivo del processo decisionale in tempo reale.
Nessuna Responsabilità: L’autore e Kriterion Quant (kriterionquant.com) declinano ogni responsabilità per qualsiasi perdita o danno, diretto o indiretto, che possa derivare dall’uso delle informazioni contenute in questo studio o da decisioni di investimento basate su di esse.
Proprietà Intellettuale: Il contenuto di questo studio è di proprietà intellettuale dell’autore e/o di Kriterion Quant. Può essere utilizzato per scopi personali e non commerciali, citando la fonte. Qualsiasi altro uso, inclusa la riproduzione, la modifica, la distribuzione o la pubblicazione senza previo consenso scritto, è vietato.
Si invita il lettore a utilizzare le informazioni qui presentate con spirito critico, come uno dei tanti strumenti a supporto di un processo decisionale di investimento ben ponderato e informato.